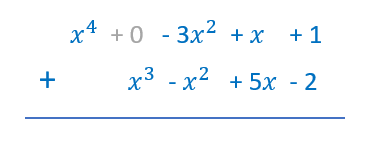22 ABRIL GRADO 8-1
niños buenos dias, vamos a tener un encuentro ahora a las 9:15 a esa hora vamos a trabajar por medio de MEET en el siguiente enlace:
Para unirte a la videollamada, haz clic en este enlace: https://meet.google.com/vja-xmxr-vqc
Si quieres unirte por teléfono, llama al +1 347-437-2857 e introduce este PIN: 417 320 287#
21 abril clases GRADO 8-2
Para unirte a la videollamada, haz clic en este enlace: https://meet.google.com/qnz-toan-xai
Si quieres unirte por teléfono, llama al +1 252-486-4007 e introduce este PIN: 230 102 407#
23 abril clase 8-1
Para unirte a la videollamada, haz clic en este enlace: https://meet.google.com/bcu-hetq-gqn
Si quieres unirte por teléfono, llama al +1 929-266-1242 e introduce este PIN: 922 932 151#
SEMANA DE MARZO 23 AL 27 2020
FASE DE APERTURA:
De acuerdo a lo que hemos visto tanto en clase como por este medio, vamos a trabajar una actividad complementaria para reforzar nuestro conocimiento y el que vamos a ver a continuación como son los polinomios.
FASE COGNITIVA:
Clases de polinomios según el número de términos
Monomio: Es un polinomio que consta de un solo monomio
Binomio: Es un polinomio que consta de dos monomios
Trinomio: Es un polinomio que consta de tres monomios
Polinomios nulos
El polinomio nulo (también llamado polinomio cero) es aquel en que todos los coeficientes son cero
Forma reducida de un polinomio
Un polinomio no nulo se dice que está escrito en forma reducida si está expresado como una suma de monomios no nulos, todos ellos de distinto grado.
Si partimos del polinomio:
Observamos que varios de los términos tienen el mismo grado. Este polinomio lo podemos simplificar haciendo las operaciones de los monomios que sean semejantes:
Esta simplificación se llama reducción de términos semejantes, y cuando realizamos esta simplificación obtenemos la forma reducida de ese polinomio
Grado de un polinomio
Grado de un polinomio no nulo
El grado de un polinomio no nulo es el grado del monomio de mayor grado que tenga el polinomio. Es decir, es el mayor exponente que tenga la letra.
Por ejemplo:
El polinomio P(x)=2x2+5x–3 tiene grado 2 (también decimos que este polinomio es de segundo grado) porque de todos los monomios que hay en este polinomio, el que tiene mayor grado es 2, y este monomio tiene grado 2.
Grado de un polinomio nulo
Un polinomio nulo (el que tiene todos los coeficientes cero), no tiene grado (porque los monomios nulos tampoco tienen grado)
Por ejemplo:
No tiene grado porque todos los monomios del polinomio son nulos, lo que hace que todo el polinomio sea nulo, y no tenga grado.
Polinomios iguales
Dos polinomios son iguales si cumplen estas dos condiciones:
1. Si tienen el mismo grado
2. Si los coeficientes de los monomios de igual grado son iguales
Por ejemplo:
Son polinomios iguales
Polinomios semejantes
Los polinomios semejantes son los que tienen las mismas partes literales
Por ejemplo:
Polinomios ordenados
Los términos de un polinomio se suelen escribir ordenados según el grado de sus monomios
El orden puede ser creciente o decreciente
Polinomios ordenados de forma creciente: los monomios se ordena de mayor a menor grado
Polinomios ordenados de forma decreciente: los monomios se ordenan de menor a mayor grado
Por ejemplo:
El polinomio P(x)=5x2+2–3x
Lo podemos ordenar de forma creciente:
o bien lo podemos ordenar de forma decreciente:
Polinomios completos y polinomios incompletos
Un polinomio completo es el que tiene todos los términos, desde el término independiente hasta el término de mayor grado.
Por ejemplo:
Un polinomio incompleto es al que le falta algún término, desde el término independiente hasta el término de mayor grado
Por ejemplo:
Polinomios homogéneos y polinomios heterogéneos
En los polinomios homogéneos, todos los términos tienen el mismo grado
Por ejemplo:
En los polinomios heterogéneos, todos los términos tienen diferente grado
Por ejemplo:
Valor numérico de un polinomio
El valor numérico de un polinomio es el número que resulta de hacer los cálculos en el polinomio cuando las letras tienen un valor determinado: sustituimos la letra por el valor de la letra y hacemos los cálculos
Por ejemplo:
El valor numérico de P(x)=2x3–5x2+3 cuando x = 2 es:
Suma y resta de polinomios en horizontal
Para hacer las operaciones en horizontal primero escribimos un polinomio y seguido en la misma línea escribimos el otro que vamos a sumar o restar. Después, agrupamos términos semejantes.
Ejemplo:
Vamos a realizar la suma. Para ello escribimos cada uno rodeado de paréntesis y con el signo de la suma entre ellos.
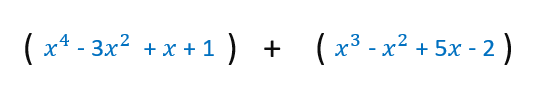Fíjate en los términos que son semejantes entre los dos polinomios.
No podemos sumar dos términos que tienen distinto grado, solo podemos agrupar los que sean semejantes y después sumar.
En la siguiente imagen están identificados los términos semejantes rodeados con el mismo color.
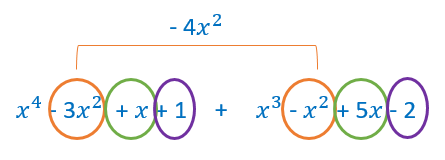Igual que hemos hecho con el término de grado 2, debemos sumar los términos de grado 1 y los términos de grado 0.
El resultado de la suma es: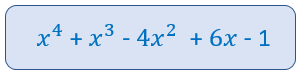
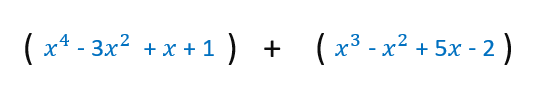
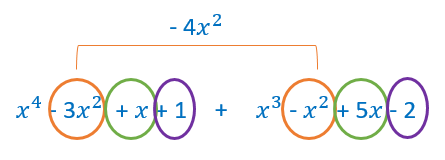
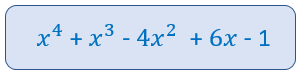
Suma de polinomios en vertical
Para hacer las sumas en vertical debemos escribir el primer polinomio ordenado. En el caso de que sea incompleto es conveniente dejar los huecos libres de los términos que falten. Después, escribimos el siguiente polinomio debajo del anterior, de manera que coincida justo debajo el término semejante al de arriba. Después, ya podemos sumar cada columna.
Ejemplo:
Vamos a ver la suma en vertical con los dos polinomios del ejemplo anterior.Fíjate en el primer polinomio. Hay que escribirlo ordenado y ver si está completo. En este caso falta el término de grado 3, entonces debemos dejar el hueco correspondiente o escribir un cero en su lugar.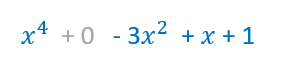
Ahora escribimos el segundo debajo del primero, de manera que coincidan los términos semejantes uno debajo de otro.
Fíjate en el primer polinomio. Hay que escribirlo ordenado y ver si está completo. En este caso falta el término de grado 3, entonces debemos dejar el hueco correspondiente o escribir un cero en su lugar.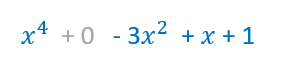Ahora escribimos el segundo debajo del primero, de manera que coincidan los términos semejantes uno debajo de otro.
Solo queda sumar cada columna, es decir, sumar los términos semejantes.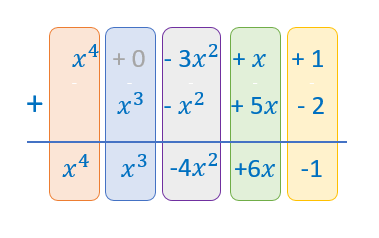
para la multiplicacion y division de polinomios dejo un link donde deben pasar a su cuadernos la informacion que esta alli.
http://laescuelaencasa.com/matematicas-2/polinomios/clase-5-multiplicacion-de-polinomios/
http://laescuelaencasa.com/matematicas-2/polinomios/clase-7-division-de-polinomios/
DEJO LINK PARA DESPEJAR DUDAS SOBRE EL TEMA.
https://www.youtube.com/watch?v=zRlJgiDVcPo
https://www.youtube.com/watch?v=xRC447bTueU
https://www.youtube.com/watch?v=XYNruwyOY_s
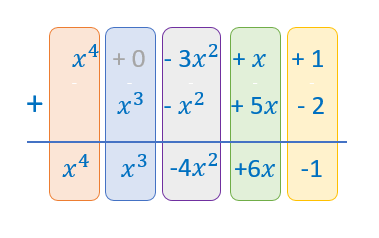
para la multiplicacion y division de polinomios dejo un link donde deben pasar a su cuadernos la informacion que esta alli.
http://laescuelaencasa.com/matematicas-2/polinomios/clase-5-multiplicacion-de-polinomios/
http://laescuelaencasa.com/matematicas-2/polinomios/clase-7-division-de-polinomios/
DEJO LINK PARA DESPEJAR DUDAS SOBRE EL TEMA.
https://www.youtube.com/watch?v=zRlJgiDVcPo
https://www.youtube.com/watch?v=xRC447bTueU
https://www.youtube.com/watch?v=XYNruwyOY_s
ACTIVIDAD EN CASA:
resolver el siguiente taller sobre polinomios.
https://drive.google.com/file/d/0B1RDWsRI51GNcjdvRnNZT05vWjA/view
Cali, marzo 21 de 2020
Apreciados estudiantes.
Cordial saludo.
Les informo que por disposición de Santa Isabel de Hungría, el día de hoy los docentes iniciamos período de vacaciones, por tal razón el plazo para la entrega de las actividades se extiende hasta el 20 de abril.
Mil gracias.
se deben enviar al correo
ksegura@arquidiocesanos.edu.co
solo se recibira hasta el 24 marzo apartir de esta fecha no se
tendran en cuenta los trabajos. (material fotográfico del cuaderno)
SÉPTIMA SEMANA: MARZO 16 AL 20
NOTA: TODO LO QUE SE PLASME EN EL BLOG DEBE ESTAR CONSIGNADO EN EL CUADERNO DE MATEMATICAS.
FASE DE APERTURA:
empezando ya los temas de álgebra, arrancamos con monomios que son, sus partes y como realizar las operaciones básicas entre monomios.
FASE COGNITIVA:
MONOMIOS
Monomios. Términos de una
expresión algebraica entera
En esta clase vamos a ver
los monomios. Fíjate en estas expresiones algebraicas:
Monomios
En estos tres casos, las
letras están sometidas solamente a operaciones de multiplicar y se llaman expresiones
monómicas o monomios, que son las que vamos a ver en esta clase
Ahora Fíjate en estas otras
expresiones algebraicas:
Polinomios
En estos casos, aunque las
letras estén sometidas a operaciones de multiplicar, también aparecen sumas o
restas. A estas expresiones algebraicas les llamamos polinomios,
y cada uno de los sumandos sería un monomio.
Expresión general de un monomio y partes
La expresión general de
cualquier monomio es:
Expresión general de un monomio
donde:
a puede ser cualquier
número racional
x puede ser cualquier letra
n puede ser cualquier
número
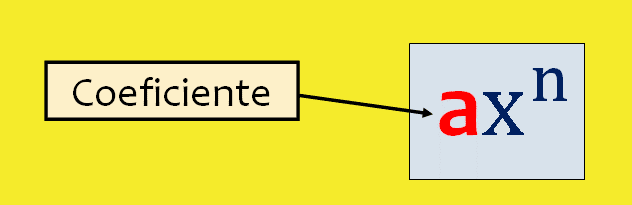
Coeficiente de un monomio
Si partimos de la expresión
general de un monomio :
Coeficiente de un monomio
El número racional a se
llama coeficiente.
El coeficiente es el número que multiplica a la
letra en el monomio
Por ejemplo:
En el monomio 2x2, el coeficiente es 2
En el monomio 23y2, el coeficiente es 2/3
Parte literal de un monomio
Si partimos de la expresión
general de un monomio:
Parte literal de un monomio
La parte literal es la letra junto con el exponente
(no incluimos el coeficiente)
Por ejemplo:
En el monomio 2x2, la parte literal es x²
En el monomio 23y2, la parte literal es y³
Grado de un monomio
Si partimos de la expresión
general de un monomio, donde el coeficiente es distinto de cero (a≠0)
El grado de ese monomio es
n
El grado de un monomio es el exponente de la letra
Por ejemplo:
En el monomio 2x2, el grado es 2. Decimos que es un
monomio de grado 2
En el monomio 23y2, el grado es 3. Decimos que es un
monomio de grado 3
Valor numérico de un monomio
El
valor numérico de un monomio es el número que resulta de hacer los cálculos en
el monomio cuando le damos a la letra un determinado valor
Ejemplo:
El valor numérico del monomio −23y2 cuando x=2
es:
−2⋅22=−2⋅4=−8
Monomios constantes
Si en un monomio cualquiera
nos encontramos que a≠0 y n=0, entonces estamos
hablando de un monomio constante, y todo ese monomio vale a
Un monomio constante es el que tiene como exponente
de la letra un cero
Monomio constante
Estos monomios se llaman
constantes porque siempre van a tener el mismo valor numérico (es decir, van a
ser sólo números, sin letras)
Ejemplos de monomios
constantes:
2x0=2
12y0=12
Monomios nulos
Si en un monomio cualquiera nos encontramos
que a=0, entonces estamos hablando de un monomio nulo, y todo ese
monomio vale cero.
Monomio nulo
Estos monomios se llaman
nulos porque siempre valen cero.
Si a = 0, entonces axn=0xn=0
Un monomio nulo no tiene
grado.
La razón de no asignar ningún grado al monomio 0 es que se puede
escribir como 0xn para cualquier númro n, es
decir, 0x,0x2,0x3,0x4,⋯
No es lo mismo no tener
grado que tener grado cero:
·
Cuando un monomio tiene
grado cero, ese es el grado del monomio: cero
·
Cuando un monomio no tiene
grado, significa que puede tener cualquier grado
Monomios semejantes
Dos o más monomios son semejantes si tienen la
misma parte literal
Monomios semejantes
Cuando dos o más monomios
tienen la misma letra y el mismo exponente en la letra, esos monomios son
semejantes
Por ejemplo:
3x³ y -2x³ son dos monomios
semejantes porque tienen la misma parte literal (tienen la misma letra elevada
al mismo exponente) aunque no tengan el mismo coeficiente
3x² y 2x³ no son monomios
semejantes porque no tienen la misma parte literal (el exponente de la letra no
es igual en los dos monomios, por lo tanto la parte literal tampoco)
2x² y 2y² no son monomios
semejantes porque no tienen la misma parte literal (la letra no es la misma,
aunque tengan el mismo exponente, por lo tanto, la parte literal tampoco es
igual en los dos monomios)
Operaciones con monomios
Suma de monomios
Solamente se pueden sumar
monomios cuando son semejantes. Si no son semejantes, no se pueden sumar.
Para sumar dos o más monomios semejantes, se suman
los coeficientes y se deja la misma parte literal.
Ejemplo: 2x3+(−3)x3
2x3+(−3)x3=(2+(−3))x3=(2−3)x3=−1x3=−x3
Resta de monomios
Solamente se pueden restar
monomios cuando son semejantes. Si no son semejantes, no se pueden restar.
Para restar dos monomios semejantes, se suma al
minuendo el opuesto del sustraendo, o lo que es lo mismo, se restan los
coeficientes y se deja la misma parte literal
Ejemplo: 2x3−(−3)x3
2x3−(−3)x3=[2−(−3)]x3=(2+3)x3=5x3
Multiplicación de monomios
Para multiplicar monomios
NO hace falta que sean semejantes
Cuando multiplicamos dos o
más monomios nos da como resultado otro monomio
Para multiplicar dos o más monomios multiplicamos
sus coeficientes y también sus partes literales
¿Cómo se multiplican las
partes literales?
·
Si tienen la misma letra,
se deja la misma letra y se suman los exponentes
Ejemplo: 2x3⋅(−3)x2
2x3⋅(−3)x2=[2⋅(−3)]x3x2=−6⋅x3+2=−6x5
·
Si tienen diferente letra,
se multiplican las letras (cada una va con su exponente)
Ejemplo: 2x3⋅(−3)y2
2x3⋅(−3)y2=2⋅(−3)x3y2=−6x3y2
División de monomios
Para dividir monomios NO
hace falta que sean semejantes, pero sí que hace falta que el divisor sea
distinto de cero.
Para dividir dos monomios,
se dividen los coeficientes y se dividen sus partes literales
¿Cómo se dividen las partes
literales?
·
Si tienen la misma letra,
se deja la misma letra y se restan los exponentes
Ejemplo: 4x32x2
4x32x2=42x3−2=2x1=2x
·
Si tienen diferente letra,
se deja como está
Ejemplo: 4x32y2
4x32y2=42x3y2=2x3y2=2x3y2
Potencia de un monomio
La potencia de un monomio
es la potencia del coeficiente por la potencia de la parte literal
Ejemplo: (−2x2)
(−2x2)=(−2)2(x2)2=4x2×2=4x4
Fijaos que al final es una
potencia de productos
EN EL SIGUIENTE LINK DEJO TUTORIAL EXPLICATIVO SOBRE LOS MONOMIOS.
ACTIVIDAD:
En el siguiente link dejo taller sobre los monomios, solo van a RESOLVER la pagina 1 y 2, en la parte de productos 4 ejercicios y en la parte de división (cocientes) 4 ejercicios también (los que ustedes escogen).
https://drive.google.com/file/d/0B1RDWsRI51GNSUdfMFAwMmttNlE/view
_______________________________________________________________________________
23 febrero 2020
niños tengan buen día.
dejo material para que lo saquen impreso y se trabaje esta semana durante las clases de matematicas.
http://www.colombiaaprende.edu.co/sites/default/files/naspublic/plan_choco/mat_9_b1_p1_est_4.pdf
TERCER PERIODO:
Unidad No.1: EXPRESIONES ALGEBRAICAS
1. Definiciones iniciales.
2. M.C.D. y M.C.M. de expresiones algebraicas.
3. Expresiones algebraicas racionales.
4. Adición y sustracción de fracciones algebraicas.
5. Multiplicación y división de fracciones algebraicas.
Unidad No. 2: ECUACIONES E INECUACIONES
1. Aplicación de las ecuaciones e inecuaciones.
Unidad No 3: GEOMETRIA
1. Longitud.
2. Área.
3. Tiempo.
SEGUNDO PERIODO
REALIZAR EL TRIANGULO DE PASCAL EN MATERIAL RECICLAJE, DEBEN LLEVAR MATERIAL A LA CLASE PARA TRABAJAR EN EL AULA.
Unidad No.1: PRODUCTOS
Y COCIENTES NOTABLES.
1.
Productos notables
2.
Triángulo de Pascal
3.
Cocientes notables
4.
División sintética
5.
Teorema del residuo
Unidad No. 2:
FACTORIZACIÓN.
1.
Factor común
2.
Factorización de binomios
3.
Factorización de trinomios
4.
Cubo perfecto de binomios
5.
Factorización completa
Unidad No 3: GEOMETRÍA.
1.
Líneas y puntos notables en un triángulo 2. Razonamiento deductivo
3.
Congruencia de triángulosPRIMER PERIODO
Unidad No.1: CONJUNTO DE LOS NÚMEROS REALES
1. Números naturales.
2. Números enteros.
3. Números racionales.
4. Números irracionales.
Unidad No. 2: EXPRESIONES ALGEBRAICAS
1. Lenguaje algebraico.
2. Monomios.
3. Polinomios.
4. Operaciones algebraicas entre monomios.
5. Operaciones algebraicas entre polinomios.
Unidad No 3: GEOMETRÍA
1. Ángulos y su clasificación,
2. Triángulos y su clasificación.
