clase de 21 de abril
Para unirte a la videollamada, haz clic en este enlace: https://meet.google.com/hkz-rriy-zen abril
Si quieres unirte por teléfono, llama al +1 518-635-7599 e introduce este PIN: 195 819 067#
semana 23 al 27 de marzo 2020
FASE DE APERTURA:
De acuerdo a lo visto anteriormente vamos a trabajar una actividad, para reforzar lo visto.
FASE COGNITIVA:
para no tener inconvenientes con la actividad deben revisar lo que ya habíamos visto o sea volver a leer para que haya una mejor compresión.
FASE METODOLOGICA:
ACTIVIDAD EN CASA
Realizar el siguiente taller que van encontrar en el link que les voy a dejar:
http://www.est.uc3m.es/esp/nueva_docencia/comp_col_get/lade/intro_estadistica/ejercicios/ejercicios4.pdf
Cali, marzo 21 de 2020

Apreciados estudiantes.
Cordial saludo.
Les informo que por disposición de Santa Isabel de Hungría, el día de hoy los docentes iniciamos período de vacaciones, por tal razón el plazo para la entrega de las actividades se extiende hasta el 20 de abril.
Mil gracias.
se deben enviar al correo
ksegura@arquidiocesanos.edu.co
solo se recibira hasta el 24 marzo apartir de esta fecha no se
tendran en cuenta los trabajos. (material fotográfico del cuaderno)
ACLARACION: LOS ESTUDIANTES DEBEN ENVIAR LAS FOTOS DEL TALLER QUE ESTABAMOS REALIZANDO EN CLASES YA RESUELTO EN SU TOTALIDAD.
SEMANA SÉPTIMA: MARZO 16 AL 20
FASE DE APERTURA:
Se le da continuidad al tema de medidas de tendencia.
FASE COGNITIVA:
SEMANA OCTAVA
Qué es un diagrama de dispersión
Dispersión se define como el grado de distanciamiento de un conjunto de valores respecto a su valor medio.
A partir de esta definición, se derivan las medidas de dispersión que aprendimos en la clase de estadística del colegio: Rango, varianza, desviación, covarianza, coeficiente de correlación, etc.
Ahora bien, el diagrama de dispersión, también conocido como gráfico de dispersión o gráfico de correlación consiste en la representación gráfica de dos variables para un conjunto de datos. En otras palabras, analizamos la relación entre dos variables, conociendo qué tanto se afectan entre sí o qué tan independientes son una de la otra.
En este sentido, ambas variables se representan como un punto en el plano cartesiano y de acuerdo a la relación que exista entre ellas, definimos su tipo de correlación.
Tipos de correlación en un gráfico de dispersión
Con base en el comportamiento que toman las variables de estudio, podemos encontrar 3 tipos de correlación: Positiva, negativa y nula.
Correlación positiva
Se presenta cuando una variable aumenta o disminuye y la otra también, respectivamente. Hay una relación proporcional. Por ejemplo para un vendedor de carros, si él vende más carros (variable 1), va a ganar más dinero (variable 2).
Correlación negativa
Se presenta cuando una variable se comporta de forma contraria o a la otra, es decir que si una variable aumenta, la otra disminuye. Hay una relación inversa proporcional. Por ejemplo para la construcción de un edificio, entre más trabajadores estén construyendo un edificio (variable 1), menos tiempo se necesitará para tenerlo listo (variable 2)
Correlación nula
Si no encuentras un comportamiento entre las variables, existe una correlación nula.
Estos son pues, los tipos de correlación más visibles. Aunque si lo miramos desde una perspectiva que evalua qué tan fuerte o débil es la correlación, encontramos otra clasificación.
El coeficiente de correlación en un diagrama de dispersión
El coeficiente de correlación nos describe cómo es la relación existente entre dos variables, en otras palabras, al conocer este número sabemos si la correlación es positiva o negativa y qué tan fuerte o débil es. Se usa la letra r para expresarla, veamos cómo:
- r=1
La correlación es positiva perfecta. Si una variable crece, la otra también lo hace en una proporción constante. Es una relación directa, por eso si trazamos una linea de ajuste esta va pasar por todos y cada uno de los puntos.
- 0
Es cuando r esta entre 0 y 1 sin llegar a ser 0 y 1. Es una correlación positiva. El grado de cercanía de 1 define qué tan directa y proporcional es la relación entre ambas variables, por ende entre más cerca esté de 0, más débil será su correlación negativa.
- r=0
La correlación es nula, es decir que no existe una relación lineal entre ambas variables. Qué tal si pruebas buscando otro tipo de relación.
- -1
Es cuando r esta entre -1 y 0 sin llegar a ser –1 y 0. Es una correlación negativa. El grado de cercanía a -1 define que tan inversa y proporcional es la relación entre ambas variables, por ende entre más cerca esté de 0, más debíl será su correlación negativa.
- r=-1
La correlación es negativa perfecta. Si una variable crece, la otra va a disminuir en proporción constante. Es una relación directa e inversa, por lo tanto una línea de ajuste va a tocar todos los puntos graficados.
Cómo hacer un diagrama de dispersión paso a paso
- Paso 1: Determina cuál es la situación. Si no entendemos qué es lo que esta ocurriendo, no podremos establecer las variables a estudiar.
- Paso 2: Determina las variables a estudiar. Si ya determinaste las variables a estudiar, es porque crees que puede existir una relación entre ellas que te permita caracterizar la situación.
- Paso 3: Recolecta los datos de las variables: Si ya los tienes, perfecto. Si no, definimos un período de tiempo para conseguir los datos de las variables antes definidas. Recuerda que los datos de las dos variables deben estar dados en el mismo período de tiempo.
- Paso 4: Ubica los valores en el eje respectivo. Por lo general, la variable independiente es aquella que no está influenciada por la otra y se ubica en el eje x. La variable dependiente que es la que se ve afectada por la otra variable se ubica en el eje y. Así pues, procedemos a ubicar los valores en el plano cartesiano de acuerdo a su variable (x, y)
- Paso 5: Determina el coeficiente de correlación: El coeficiente de correlación debe verse reflejado en la forma que toma el gráfico de dispersión. Es el cociente de la covarianza y la multiplicación de la desviación típica de las dos variables. Con excel logramos calcularlo de manera muy simple.
- Paso 6: Analizamos: Con base en el coeficiente y en el gráfico, definimos cuál es la relación de las dos variables y tomamos las decisiones pertinentes.
Ejemplo de diagrama de dispersión
Vamos a ver desde una problemática empresarial, un ejemplo resuelto de diagrama de dispersión para el área de calidad.
Imagina que una litográfica está abriendo una nueva área de producción para la impresión de posters, y en este momento se encuentra haciendo todos los ensayos y pruebas para determinar la cantidad de tinta de cada color que deberían tener las maquinas.
Como prueba inicial, han decidido establecer la relación de errores de impresión según el grado de llenado de los recipientes de tinta de la máquina.
Bien, definida la situación, iniciamos desde el paso 2:
Las variables a estudiar para este ejemplo de grafico de dispersión en calidad son:
- Cantidad de tinta en litros
- Número de errores de impresión
Para el paso 3, comenzamos a recolectar las variables. En nuestro caso, el departamento de control de calidad hace 50 corridas o pruebas durante 5 días continuos.
Los resultados, a continuación:
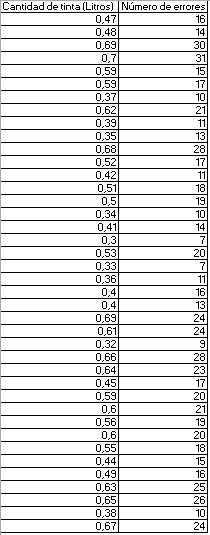

Para el paso 4 ubicamos los ejes según las variables que tenemos. Al estar el número de errores influenciado por la cantidad de tinta, lo ubicamos como el eje y. Por consiguiente, el eje x es la cantidad de tinta. Ahora sí, hacemos el gráfico de dispersión.
Paso 5: Determinamos el coeficiente de correlación. En excel lo calculamos con la formula COEF.DE.CORREL. Para nuestro ejemplo resuelto, obtenemos 0,94, ¿se ve esto reflejado en el gráfico? Por supuesto que si, fíjate que los puntos están muy cerca unos de los otros, lo que indica que los valores se correlacionan fuertemente, es decir que la relación entre un aumento en los litros de tinta, impacta directamente en el número de errores en la impresión de posters. De hecho se hace evidente si miramos la tabla, no hay grandes saltos entre datos si miramos el número de errores.
Paso 6: Analizamos. Evidentemente hay una relación positiva fuerte entre la cantidad de tinta con la que se carga el tubo de la máquina y el número de errores generados en la impresión de los posters. Un paso siguiente para un problema de este tipo, sería buscar la forma de aprovechar la capacidad restante de la máquina, por ejemplo usar más tubos y más pequeños.
FASE METODOLOGICA
ACTIVIDAD EN CASA
Realiza dos ejemplos de diagramas de dispersión.
_________________________________________________________________________________
25 febrero 2020
para la proxima clase traer impreso el siguiente taller.
http://aprende.colombiaaprende.edu.co/sites/default/files/naspublic/ContenidosAprender/G_11/M/SM/SM_M_G11_U05_L03.pdf
TERCER PERIODO:
FUNCIÓN DE PROBABILIDAD
1. Variables aleatorias discretas y continuas
2. Función de probabilidad de variables discretas
3. Propiedades de la función de probabilidad
SEGUNDO PERIODO:
UNIDAD 1: PROBABILIDAD CONDICIONAL
1. Eventos dependientes e independientes
2.
Probabilidad condicional
3. Teorema de BayesPRIMER PERIODO
UNIDAD 1: MEDIDAS Y CORRELACIÓN
1. Medidas de tendencia central, posición y dispersión
2. Diagramas de dispersión
3. Covarianza
4. Coeficiente de correlación lineal




